Understanding Diffusion Models

In recent years, diffusion models have taken the AI world by storm, offering a new and powerful way to generate realistic images, audio, and even video from scratch. In this post, we’ll dive into how these models work.

Intuition

A diffusion model is a type of generative model that learns how to gradually add random noise to some data (i.e. the forward process) and learns to gradually reverse this random noise (i.e. the reverse process) to generate a sample that resembles one drawn from a real-world distribution.

Image generated by Imagen using the prompt "A cute racoon teaching a class of garden animals some concepts about machine learning".

Since it is a generative model, it can capture the underlying distribution of the data that it was trained with. This can be used to effectively generate a large number of samples that resemble the training data. A common application of this is for text-to-image generation with models such as Imagen and DALL-E, in which a text prompt is used to generate an image.

Forward and Reverse Processes Intuition

Let’s set up an analogy to understand the forward and reverse processes.

• Suppose I give you a Jackson Pollock painting, and ask you to add “noise” to it. That sounds pretty simple – you may take a bucket of paint and throw it at the painting. This is similar to the forward process.
• Next, I find another another Jackson Pollock painting and I throw a bucket of paint on it. I ask you to remove all the paint that I threw and recover the original painting. This is clearly a much harder task because it would be nearly impossible to distinguish which paint was thrown on and which was part of the original painting. While your best efforts may bring you close to the original painting, you would probably never be able to recover it. This is similar to the reverse process.

This difficult task of recovering the data (i.e. the reverse process) from noise (i.e. the paint) is what diffusion models are trying to learn.

Learning Intuition

Suppose that we want to generate human faces. How do we go about learning a diffusion model that does this? As described in the previous section, the forward process would involve adding random noise to images of faces, and the reverse process would involve generating faces from random noise.

We collect a dataset of human faces, and then follow the steps below.

1. Sample a random image from the dataset.
2. Add some random noise to the image to generate a noisy image (the forward process).
3. Feed noisy image to the model, and have it predict the noise (the reverse process).
4. Compute the loss between the predicted noise and actual noise added in Step 2.
5. Update the model parameters so that the model is more likely to predict the correct noise.
6. Repeat Step 1 - Step 5 until the model is good at predicting the noise in a noisy image.

Once this is done, we can use it to generate new images of human faces.

Inference Intuition

Source: Image generation with diffusion models using Keras and TensorFlow

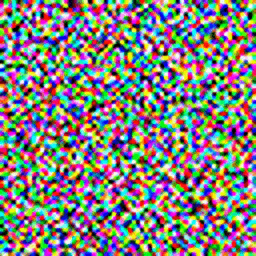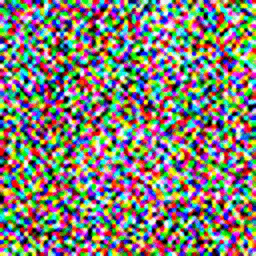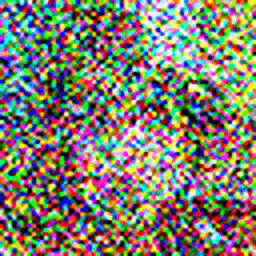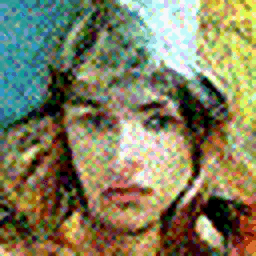
The process of generating a new image of a human face involves incrementally following the reverse process.

1. Sample some random noise.
2. Feed a noisy image to the model, and have it predict the noise in the image.
3. Use the predicted noise to sample a less noisy image.
4. Repeat Step 2 - Step 3 until the model outputs an image that looks like a human face.

Derivation

In this section, we derive the math behind diffusion models, as outlined in the original denoising diffusion probabilistic models (DDPM) paper .

Problem Setup

Assume we have a dataset $\mathcal{D} = x^{(1)}, x^{(2)}, …, x^{(n)}$ with $n$ images of human faces. Let $q(\textbf{x}_0)$ denote the underlying data distribution from which $\mathcal{D}$ is generated. We choose some distribution $p_{\theta}(\textbf{x}_0)$ for which sampling $\textbf{x}_0 \sim p_{\theta}(\textbf{x}_0)$ is tractable. Our goal is to learn $\theta$ such that $p_{\theta}(\textbf{x}_0) \approx q(\textbf{x}_0)$.

Forward Process Derivation

Source

The forward process is modeled as a Markov chain that incrementally adds noise to the data. The process runs for $t = 0, 1, 2, …, T$ steps, with $\textbf{x}_t$ denoting the data at step $t$. Given data $\textbf{x}_{t-1}$, the forward process generates $\textbf{x}_{t}$ by adding noise to $\textbf{x}_{t-1}$. We define the probability of transitioning from state $\textbf{x}_{t-1}$ to $\textbf{x}_{t}$ as $q(\textbf{x}_t \mid \textbf{x}_{t-1})$.

Markov property

The Markov property states that for a Markov chain with a sequence of random variables $X_1, X_2, X_3, …$, the probability of moving to the next state depends only on the current state, and not on the previous states.

$P(X_{n+1} = x \mid X_1 = x_1, X_2 = x_2, …, X_n = x_n) = P(X_{n+1} = x \mid X_n = x_n)$

Because of the Markov property, the probability of each state is only dependent on the probability of its previous state, and so,

\[\begin{align*} q(\textbf{x}_{1: T}) &= q(\textbf{x}_0) \cdot q(\textbf{x}_1 \mid \textbf{x}_0) \cdot q(\textbf{x}_2 \mid \textbf{x}_1) \cdot \ldots \cdot q(\textbf{x}_{T} \mid \textbf{x}_{T-1})\\ &= q(\textbf{x}_0) \prod_{t = 1}^T q(\textbf{x}_t \mid \textbf{x}_{t-1}) \end{align*}\]

We can formulate this as adding Gaussian noise with some known variance schedule $ 0 < \beta_1 < \ldots < \beta_t < \ldots < \beta_T$ to $\textbf{x}_{t-1}$, creating a new variable $\textbf{x}_{t}$ with distribution $q(\textbf{x}_t \mid \textbf{x}_{t-1})$. This variance schedule is chosen to ensure that $\textbf{x}_T$ is nearly an isotropic Gaussian i.e. $q(\textbf{x}_T) \sim \mathcal{N}(\textbf{0}, \textbf{I})$.

\[q(\textbf{x}_t \mid \textbf{x}_{t-1}) = \mathcal{N}(\textbf{x}_t; \sqrt{1 - \beta_t}\textbf{x}_{t-1}, \beta_t \textbf{I})\]

The mean of this distribution is some known transformation of the image in the previous step, which we also know. The variance is fixed, and the constant is multiplied by the identity matrix, which means that the noise in different parts of the image is independent of each other.

Reparameterization trick for normal distributions

Suppose $X$ is a random variable such that $X \sim \mathcal{N}(0, \textbf{I})$. Define a new random variable $Y = \mu + \sigma X$. Then,

\[\begin{align*} \mathbb{E}[Y] &= \mathbb{E}[\mu + \sigma X] = \mu + \sigma \cdot \mathbb{E}[X] = \mu\\ \text{Var}[Y] &= \text{Var}[\mu + \sigma X] = \sigma^2 \cdot \text{Var}[X] = \sigma^2 \end{align*}\]

We use the reparameterization trick to reparameterize $Y$ in terms of $X$.

Using the reparameterization trick, we can rewrite $\textbf{x}_{t}$ as the following, where $\epsilon_{t-1} \sim \mathcal{N}(0, \textbf{I})$.

\[\textbf{x}_{t} = \sqrt{1 - \beta_t} \cdot \textbf{x}_{t-1} + \sqrt{\beta_t} \cdot \epsilon_{t-1}\]

We now have a way to compute $\textbf{x}_{t}$ using $\textbf{x}_{t-1}$, but to compute $\textbf{x}_{t-1}$ we need $\textbf{x}_{t-2}$, and so on until $\textbf{x}_0$. It turns out that we can rewrite the equation above to only depend only on $\textbf{x}_{0}$, so we can skip all the intermediate steps.

Let’s define some terminology first to simplify this process.

\[\begin{align*} \alpha_t &= 1 - \beta_t\\ \bar{\alpha}_t &= \prod_{i = 1}^t \alpha_i = \alpha_1 \cdot \alpha_2 \cdot \ldots \alpha_t \end{align*}\]

Sum of two Gaussians is a Gaussian

Let $X \sim \mathcal{N}(\mu_x, \sigma^2_x)$ and $Y \sim \mathcal{N}(\mu_y, \sigma^2_y)$. Then,

\[X + Y \sim \mathcal{N}(\mu_x + \mu_y, \sigma^2_x + \sigma^2_y)\]

Using this terminology and the Gaussian property, we can rewrite $\textbf{x}_{t}$ recursively.

\[\begin{align*} \textbf{x}_{t} &= \sqrt{\alpha_t} \cdot \textbf{x}_{t-1} + \sqrt{1 - \alpha_t} \cdot \epsilon_{t-1}\\ &= \sqrt{\alpha_t} \cdot (\sqrt{\alpha_{t-1}} \cdot \textbf{x}_{t-2} + \sqrt{1 - \alpha_{t-1}} \cdot \epsilon_{t-2}) + \sqrt{1 - \alpha_t} \cdot \epsilon_{t-1}\\ &= \sqrt{\alpha_t \cdot \alpha_{t-1}} \cdot \textbf{x}_{t-2} + \sqrt{\alpha_t \cdot (1 - \alpha_{t-1})} \cdot \epsilon_{t-2} + \sqrt{1 - \alpha_t} \cdot \epsilon_{t-1}\\ &= \sqrt{\alpha_t \cdot \alpha_{t-1}} \cdot \textbf{x}_{t-2} + \sqrt{\alpha_t \cdot (1 - \alpha_{t-1}) + 1 - \alpha_t} \cdot \bar{\epsilon}_{t-2}\\ &= \sqrt{\alpha_t \cdot \alpha_{t-1}} \cdot \textbf{x}_{t-2} + \sqrt{1 - \alpha_t \cdot \alpha_{t-1}} \cdot \bar{\epsilon}_{t-2}\\ & \qquad \vdots\\ &= \sqrt{\bar{\alpha}_t} \cdot \textbf{x}_0 + \sqrt{1 - \bar{\alpha}_t} \cdot \bar{\epsilon}_{0} \end{align*}\]

Now, we can go from the original image $\textbf{x}_0$ to the noisy image $\textbf{x}_t$ at any step $t$ efficiently in closed form. In other words (again using the reparameterization trick),

\[q(\textbf{x}_t \mid \textbf{x}_0) = \mathcal{N}(\textbf{x}_t; \sqrt{\bar{\alpha}_t} \textbf{x}_0, (1 - \bar{\alpha}_t) \textbf{I})\]

What we’re really interested in, though, is how we can go from a noisy image to a realistic image, which we will derive with the reverse process.

Reverse Process Derivation

Source

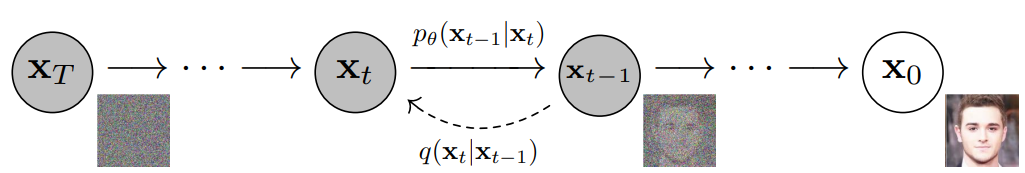
Similar to the forward process, the reverse process is also modeled as a Markov chain but we now gradually denoise data to generate a realistic image $\textbf{x}_0$.

If sampling from $q(\textbf{x}_{t-1} \mid \textbf{x}_t)$ was possible, we could have easily generated $\textbf{x}_0$. However, sampling from $q(\textbf{x}_{t-1} \mid \textbf{x}_t)$ is intractable. To properly model this reverse transition, we need to account for the fact that $\textbf{x}_{t}$ is not just a noisy version of $\textbf{x}_{t-1}$, but is also influenced by the earlier steps in the diffusion chain. In other words, the reverse process involves an intricate dependency on all the noise added at every earlier step in the forward process, which makes the true reverse process highly complex and difficult to model directly.

We therefore need to learn a model $p_\theta$ that can approximate these conditional probabilities to run the reverse diffusion process. We define the probability of transitioning from state $\textbf{x}_{t}$ to $\textbf{x}_{t-1}$ as $p_\theta(\textbf{x}_{t-1} \mid \textbf{x}_{t})$.

Because of the Markov property,

\[p_\theta(\textbf{x}_{1:T}) = p_\theta(\textbf{x}_{T}) \prod_{t=1}^T p_\theta(\textbf{x}_{t-1} \mid \textbf{x}_{t})\]

We formulate this as sampling $\textbf{x}_{t-1}$ from a Gaussian distribution with learned mean $\mathbf{\mu_\theta}(\textbf{x}_{t}, t)$ and learned variance $\mathbf{\Sigma_\theta}(\textbf{x}_{t}, t)$.

\[p_\theta(\textbf{x}_{t-1} \mid \textbf{x}_{t}) = \mathcal{N}(\mathbf{\mu_\theta}(\textbf{x}_{t}, t), \mathbf{\Sigma_\theta}(\textbf{x}_{t}, t))\]

In order to derive this, it’s worth noting that the reverse conditional that we previously said was intractable, becomes tractable when conditioning on $\textbf{x}_{0}$. This is because it is now constrained to be consistent with the known data distribution $\textbf{x}_{0}$, and we do not need to consider all possible noise configurations in the same way we would without conditioning on $\textbf{x}_{0}$.

\[q(\textbf{x}_{t-1} \mid \textbf{x}_t, \textbf{x}_0) = \mathcal{N}(\mathbf{\tilde{\mu}_q}(\textbf{x}_{t}, t), \mathbf{\tilde{\Sigma}_q}(\textbf{x}_{t}, t))\]

We want $p_\theta(\textbf{x}_{t-1} \mid \textbf{x}_{t})$ to be as close as possible to $q(\textbf{x}_{t-1} \mid \textbf{x}_t, \textbf{x}_0)$. Intuitively, this makes sense. If the learned reverse process is supposed to subtract away the noise, then whenever we have a specific $\textbf{x}_0$, it should substract the noise away exactly as the exact reverse process would have.

Bayes’ theorem

Given events $A$ and $B$, where $P(B) \neq 0$,

\[P(A \mid B) = \frac{P(B \mid A) \cdot P(A)}{P(B)}\]

By Bayes’ theorem,

\[\begin{align*} q(\textbf{x}_{t-1} \mid \textbf{x}_t, \textbf{x}_0) = q(\textbf{x}_t, \textbf{x}_0 \mid \textbf{x}_{t-1}) \cdot \frac{q(\textbf{x}_{t-1} \mid \textbf{x}_0)}{q(\textbf{x}_t \mid \textbf{x}_0)} \end{align*}\]

Note that this is a product of three Gaussians, each of which can be represented by their corresponding density functions.

Representing Gaussian by it’s density function

If $X$ is a normal random variable with mean $\mu$ and variance $\sigma^2$ i.e. $X \sim \mathcal{N}(\mu, \sigma^2)$, then

\[\begin{align*} f_X(x) &= \frac{1}{\sqrt{2\pi\sigma^2}} \exp \{ - \frac{(x - \mu)^2}{2\sigma^2} \}\\ &\propto \exp \{ - \frac{1}{2} \left( \frac{(x - \mu)^2}{\sigma^2} \right) \} \end{align*}\]

Therefore,

\[\begin{align*} q(\textbf{x}_{t-1} \mid \textbf{x}_t, \textbf{x}_0) &\propto \exp\{ -\frac{1}{2} ( \frac{(\textbf{x}_t - \sqrt{\alpha_t} \textbf{x}_{t-1})^2}{1 - \alpha_t} + \frac{(\textbf{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}} \textbf{x}_0)^2}{1 - \bar{\alpha}_{t-1}} - \frac{(\textbf{x}_t - \sqrt{\bar{\alpha}_t} \textbf{x}_0)^2}{1 - \bar{\alpha}_t} ) \}\\ &\qquad \vdots\\ &= \exp \{ -\frac{1}{2} \left( (\frac{\alpha_t}{1 - \alpha_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) \textbf{x}_{t-1}^2 - (\frac{2 \sqrt{\alpha_t}}{1 - \alpha_t} \textbf{x}_{t} + \frac{2 \sqrt{\bar{\alpha}}_{t-1}}{1 - \bar{\alpha}_{t-1}} \textbf{x}_0) \textbf{x}_{t-1} + C(\textbf{x}_{t}, \textbf{x}_0) \right) \} \end{align*}\]

$C(\textbf{x}_{t}, \textbf{x}_0)$ is a function not involving $\textbf{x}_{t-1}$ and is therefore not relevant. Again representing this as a Gaussian (except now in reverse), we have $\mathbf{\tilde{\mu}_q}(\textbf{x}_{t}, t)$ and $\mathbf{\tilde{\Sigma}_q}(\textbf{x}_{t}, t)$.

\[\mathbf{\tilde{\mu}_q}(\textbf{x}_{t}, t) = \frac{\sqrt{\alpha_t} (1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \textbf{x}_{t} + \frac{\sqrt{\bar{\alpha}_{t-1}} (1 - \alpha_t)}{1 - \bar{\alpha}_t} \textbf{x}_{0}\]

In the forward process, we showed that $\textbf{x}_t = \sqrt{\bar{\alpha}_t} \cdot \textbf{x}_0 + \sqrt{1 - \bar{\alpha}_t} \cdot \mathbf{\epsilon}_t$. Substituting in $\textbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}} \cdot \left(\textbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \cdot \mathbf{\epsilon}_t \right)$, we get

\[\mathbf{\tilde{\mu}_q}(\textbf{x}_{t}, t) = \frac{1}{\sqrt{\alpha_t}} \left( \textbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}{}} \mathbf{\epsilon}_t \right)\]

We also obtain $\mathbf{\tilde{\Sigma}_q}(\textbf{x}_{t}, t)$.

\[\begin{align*} \mathbf{\tilde{\Sigma}_q}(\textbf{x}_{t}, t) &= 1 / (\frac{\alpha_t}{1 - \alpha_t} + \frac{1}{1 - \bar{\alpha}_{t-1}})\\ &= \frac{(1 - \bar{\alpha}_{t-1}) (1 - \alpha_t)}{1 - \bar{\alpha}_t} \end{align*}\]

We’ve shown how $\textbf{x}_{t-1}$ can be sampled given some $\textbf{x}_{t}$ and $\textbf{x}_{0}$ by sampling from $q(\textbf{x}_{t-1} \mid \textbf{x}_t, \textbf{x}_0) = \mathcal{N}(\mathbf{\tilde{\mu}_q}(\textbf{x}_{t}, t), \mathbf{\tilde{\Sigma}_q}(\textbf{x}_{t}, t))$. However, for our reverse process, what we really want is to be able to do this without any dependence on $\textbf{x}_0$, by sampling $\textbf{x}_{t-1}$ from our learned distribution $p_\theta(\textbf{x}_{t-1} \mid \textbf{x}_{t}) = \mathcal{N}(\mathbf{\mu_\theta}(\textbf{x}_{t}, t), \mathbf{\Sigma_\theta}(\textbf{x}_{t}, t))$. We discuss how to learn this in the next section.

Learning Derivation

We want $p_\theta(\textbf{x}_{t-1} \mid \textbf{x}_{t})$ to be as close as possible to $q(\textbf{x}_{t-1} \mid \textbf{x}_t, \textbf{x}_0)$, and so $\mathbf{\mu_\theta}(\textbf{x}_{t}, t)$ must be as close as possible to $\mathbf{\tilde{\mu}_q}(\textbf{x}_{t}, t)$, and $\mathbf{\Sigma_\theta}(\textbf{x}_{t}, t)$ as close as possible to $\mathbf{\tilde{\Sigma}_q}(\textbf{x}_{t}, t)$ .

Since $\mathbf{\tilde{\Sigma}_q}(\textbf{x}_{t}, t)$ is a constant for any $t$ without any dependence on other variables, we can just use what we know about $q(\textbf{x}_{t-1} \mid \textbf{x}_t, \textbf{x}_0)$.

\[\mathbf{\Sigma_\theta}(\textbf{x}_{t}, t) = \mathbf{\tilde{\Sigma}_q}(\textbf{x}_{t}, t) = \frac{(1 - \bar{\alpha}_{t-1}) (1 - \alpha_t)}{1 - \bar{\alpha}_t}\]

However, $\mathbf{\tilde{\mu}_q}(\textbf{x}_{t}, t)$ has a dependence on $\epsilon_t$, which is the noise that gave rise to $\textbf{x}_{t}$ from $\textbf{x}_0$ in the forward process. This is what we will be learning. We can do this by learning a function parameterized by $\theta$, typically a UNet. In other words,

\[\begin{align*} \mathbf{\mu_\theta}(\textbf{x}_{t}, t) &= \frac{1}{\sqrt{\alpha_t}} \left( \textbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \mathbf{\epsilon}_\theta(\textbf{x}_t, t) \right), && \text{where $\mathbf{\epsilon}_\theta(\textbf{x}_t, t) = \text{UNet}_\theta(\textbf{x}_t, t)$} \end{align*}\]

Let’s map this theory back to the intuition we set up earlier for learning the model.

1. Sample a random image from the dataset.
   • $x_0 \sim \mathcal{D}$
2. Add some random noise to the image to generate a noisy image (the forward process).
   • $t \sim \text{Uniform}(1, \ldots, T)$
   • $\mathbf{\epsilon} \sim \mathcal{N}(\mathbf{0}, \textbf{I})$
   • $\textbf{x}_t = \sqrt{\bar{\alpha}_t} \cdot \textbf{x}_0 + \sqrt{1 - \bar{\alpha}_t} \cdot \mathbf{\epsilon}$
3. Feed noisy image to the model, and have it predict the noise (the reverse process).
   • $\mathbf{\epsilon}_\theta(\textbf{x}_t, t) = \text{UNet}_\theta(\textbf{x}_t, t)$
4. Compute the loss between the predicted noise and actual noise added in Step 2.
   • $\ell_t(\theta) = \| \mathbf{\epsilon} - \mathbf{\epsilon}_\theta(\textbf{x}_t, t) \|^2$
5. Update the model parameters so that the model is more likely to predict the correct noise.
   • $\theta = \theta - \nabla_\theta \ell_t(\theta)$
6. Repeat Step 1 - Step 5 until the model is good at predicting the noise in a noisy image.

Inference Derivation

Similarly, we can map the theory back to the intuition we set up earlier for running inference with the learned model.

1. Sample some random noise.
   • $\textbf{x}_{T} \sim \mathcal{N}(\mathbf{0}, \textbf{I})$
2. Feed a noisy image to the model, and have it predict the noise in the image.
   • $\mathbf{\epsilon}_t \sim \mathcal{N}(\mathbf{0}, \textbf{I})$
   • $\mathbf{\epsilon}_\theta(\textbf{x}_t, t) = \text{UNet}_\theta(\textbf{x}_t, t)$
3. Use the predicted noise to sample a less noisy image.
   • $\mathbf{\hat{\mu}_\theta}(\textbf{x}_{t}, t) = \frac{1}{\sqrt{\alpha_t}} \left( \textbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \mathbf{\epsilon}_\theta(\textbf{x}_t, t) \right)$
   • Using the reparameterization trick, since $p_\theta(\textbf{x}_{t-1} \mid \textbf{x}_{t}) = \mathcal{N}(\mathbf{\hat{\mu}_\theta}(\textbf{x}_{t}, t), \mathbf{\Sigma_\theta}(\textbf{x}_{t}, t))$, we have $\textbf{x}_{t-1} = \mathbf{\hat{\mu}_\theta}(\textbf{x}_{t}, t) + \mathbf{\Sigma_\theta}(\textbf{x}_{t}, t) \cdot \mathbf{\epsilon}_t$
4. Repeat Step 2 - Step 3 until the model outputs an image that looks like a human face.
   • $\textbf{x}_{T-1} = \mathbf{\hat{\mu}_\theta}(\textbf{x}_{T}, T) + \mathbf{\Sigma_\theta}(\textbf{x}_{T}, T) \cdot \mathbf{\epsilon}_T$
   • $\textbf{x}_{T-2} = \mathbf{\hat{\mu}_\theta}(\textbf{x}_{T-1}, T-1) + \mathbf{\Sigma_\theta}(\textbf{x}_{T-1}, T-1) \cdot \mathbf{\epsilon}_{T-1}$
   • $\ldots$
   • $\textbf{x}_{0} = \mathbf{\hat{\mu}_\theta}(\textbf{x}_{1}, 1) + \mathbf{\Sigma_\theta}(\textbf{x}_{1}, 1) \cdot \mathbf{\epsilon}_1$

Acknowledgements

The content for this post was heavily inspired by a number of different sources, including the original paper Denoising Diffusion Probabilistic Models by Ho et al, as well as a number of other blog posts on this topic like What are Diffusion Models? by Lilian Weng, Diffusion Models by Andrew Chan, and Diffusion Models from Scratch by Michael Wornow.